Когато повечето от нас виждат машина, която дърпа мъчно, как се отдръпва по туристическия тротоар, се сещаме за сладка, сладка захар. Жан-Люк Тифо мисли за сладко, сладко математика. Като приложен математик от Университета на Уисконсин-Медисън, Thiffeault се интересува особено от начина, по който материали като тафи се смесват: В машината бонбоните се разтягат и сгъват отново и отново, за да включат въздух и да развият своята лека, дъвчаща текстура. Докато се дърпа, оригиналният правоъгълник на тафи се разтяга все повече и повече - дължината му нараства експоненциално с едно и също съотношение всеки път. Това съотношение на разтягане е това, което интересува Thiffeault.
Свързано съдържание
- Разтопен шоколад, 3D печатни гуми и други очарователни патенти за бонбони
Когато човек издърпа нелепо, обикновено ще вземе бучката бонбони и ще я опъне върху кука, като сближи двата края. Тогава те ще вземат това сгънато парче и ще го разтеглят отново върху куката, удвоявайки дължината и т.н. С други думи, „Човешкият начин на работа е коефициент на умножение 2“, казва Тиф. Механичните тегличи могат да се справят по-добре, често дават по-големи, екзотични ирационални числа, като техните разтягащи фактори.
Оказва се, че трудното дърпане може да се моделира от абстрактно математическо поле, известно като топологична динамика, по същество изследване на дългосрочни, мащабни промени във времето в математическо пространство. (Ако думата топологично звучи познато, тя беше в новините наскоро като част от тазгодишната Нобелова награда по физика.) Същата математика, която описва издърпването, също има по-сериозни приложения: много индустриални процеси, включително продухване на стъкло и приготвяне на лекарства, изискват вискозни течности, които трябва да се смесват по начини, които приличат повече на теглене, отколкото разбъркване на сметана в кафе. „Ако се опитвате да разбърквате наистина вискозни неща, като пастата от фармацевтичната индустрия, не можете просто да ги разклатите“, казва Thiffeault. „Не е като смесване на боя.“
Thiffeault отдавна е разбрал изтръпването като пример за вискозно смесване, но едва наскоро всъщност е вникнал в историята на taffy-pullers, за да разкрие своите математически тайни. Резултатът от екскурзията в исторически патенти е последната му статия „Математическа история на нестабилни манипулатори“, публикувана на сървъра за предпечат arXiv през юли.
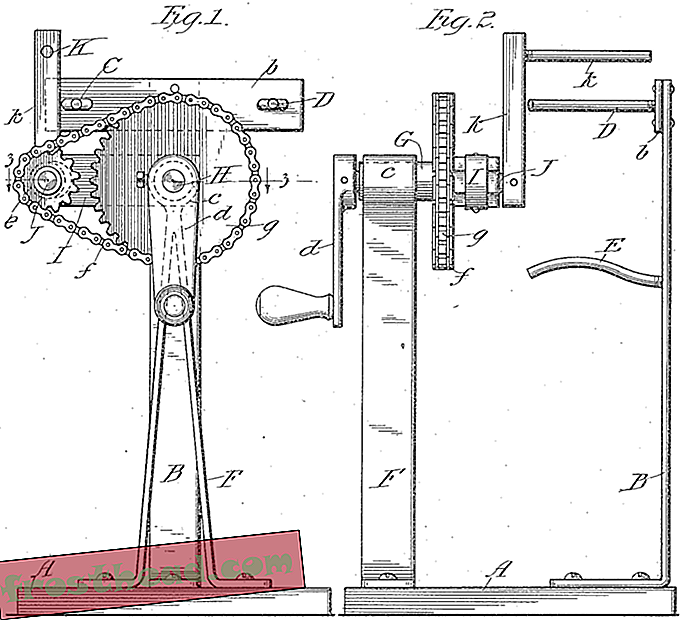Изображение от патентен машинен патент от 1916 г., който се появява в изследването на Thiffeault. По-конкретно, зоната, довела до дълбокото му гмуркане с тафи-пулър, е изследването на така наречените псевдо-Аносов карти. Псевдо-Аносов е фантастичен начин за описване на процес, при който двуизмерната форма е опъната експоненциално в една посока, докато се свива в другата. Математически, изследването на псевдоаносовските карти е сравнително ново. „През 70-те и 80-те години хората много се опитваха да намерят примери“, казва Тиф. По ирония на съдбата, те са били там през цялото време в патенти за тежки манипулатори. „Тъй като математиците никога не са разглеждали тази литература, те никога не биха разбрали, че съществуват“, казва той.
Докато той се разресваше чрез патенти с твърди съвети, Тифро се натъкна на правна битка, която стигна чак до Върховния съд. Спорен по делото от 1921 г. Hildreth срещу Mastoras е колко широко трябва да се тълкува патентът от 1900 г. за измама. Тоест: по-късен модел, направен от някой друг, беше само незначително подобрение, или беше различно устройство? Съществена част от аргумента беше колко различен е патентът от 1900 г. от предшественика от 1893 г. (който вероятно никога не е произведен). Становището на съда, автор на главния съдия Уилям Хауърд Тафт, „показва силно разбиране на топологичната динамика“, пише Тиф в своята статия.
Съдът призна, че по-ранното устройство - което имаше само две куки - не би могло да разтегне тъканта до експоненциалната степен, необходима за ефективно създаване на сладкарски изделия. Становището на Taft гласи:
Само с две кукички не можеше да има прилепване на бонбоните, тъй като нямаше трети щифт, който да задейства отново бонбона, докато той се държеше между другите две щифтове. Движението на двете щифтове в концентрични кръгове може да го разтегне донякъде и да го раздвижи, но не би го издърпало в смисъла на изкуството.
Thiffeault пише: „Становището на Върховния съд показва основното разбиране, че са необходими поне три пръчки, за да се постигне някакъв бърз растеж.“
Thiffeault казва, че днес се използват два стандартни теглича, едно с три пръта и едно с четири. Случва се да имат същия коефициент на разтягане. Той е свързан с така нареченото съотношение на среброто 1+ √2 или около 2.414, малко по-малко светещ братовчед с по-известното златно съотношение.
Фактът, че двата стандартни теглича се разтягат със съотношението на среброто е интересен, защото съотношението сребро е - в точен математически смисъл - оптимално. Въпреки това Thiffeault предупреждава, че не е толкова лесно да се класират различни хапчета, дори когато знаете техните фактори на разтягане: „Има ябълки и портокали аспект към него, който е доста трудно да се заобиколи“, казва той. Един буталник може да има повече пръчки и да отнеме повече време, за да се върне в първоначалното си състояние, отколкото друг, или може да изисква по-голям въртящ момент или по-сложно предаване. Макар че математиката дава известна представа за това колко добре се дърпат, това не разказва цялата история.
Изследванията на Thiffeault в тафи-пулс вдъхновиха него и неговия студент Алекс Фланаган да създадат свой собствен модел. Те искаха да видят дали могат да увеличат ефективността, без да променят много предавките, и в крайна сметка направиха нов 6-прът на основата на предавката на стандартния 4-прът. "Причината, поради която успяхме да го направим, е, че имаме математика сега", казва Тиф. Те биха могли да моделират широко машината на компютъра и да заобиколят голяма част от опита и грешките с реални физически устройства, които по-ранните изобретатели трябваше да правят. Устройството с 6 пръта, което все още е само прототип, се разтяга доста два пъти повече от стандартните пулвери във всеки цикъл.
Досега производителите на нестабилни машини не са пребили точно вратата на Thiffeault, за да получат съветите му за оптимизиране на дизайна им - Big Taffy очевидно се задоволява със своето еластично състояние - но той се надява, че неговите методи биха могли да окажат ефект в други индустрии. Освен духането на стъкло, едно логично място за оптимизиране на смесването е фармацевтичната индустрия. В крайна сметка смесването на витамини и лекарства изисква изключително висок качествен контрол: Производителите са "готови да платят много пари за перфектно смесване", защото "не могат да понасят един лош мултивитамин от 1000", казва Thiffeault. Така че някой ден фармацевтите може да излъчат сладък вик на посветените накрайници, които не са в състояние.
След това отново, това може да е малко разтягане.
